Pentagono preso di mira

Buon pomeriggio Prof Scorsipa, credo di averlo risolto , X viene 160 ?

Buon pomeriggio Prof Scorsipa le invio la risoluzione del problema da lei proposto.



PROBLEMA PENTAGONO PRESO DI MIRA

Soluzione proposta da Mario Solinas

https://i.servimg.com/u/f67/20/20/95/54/proble10.png ( link per vedere la figura)


Risoluzione :

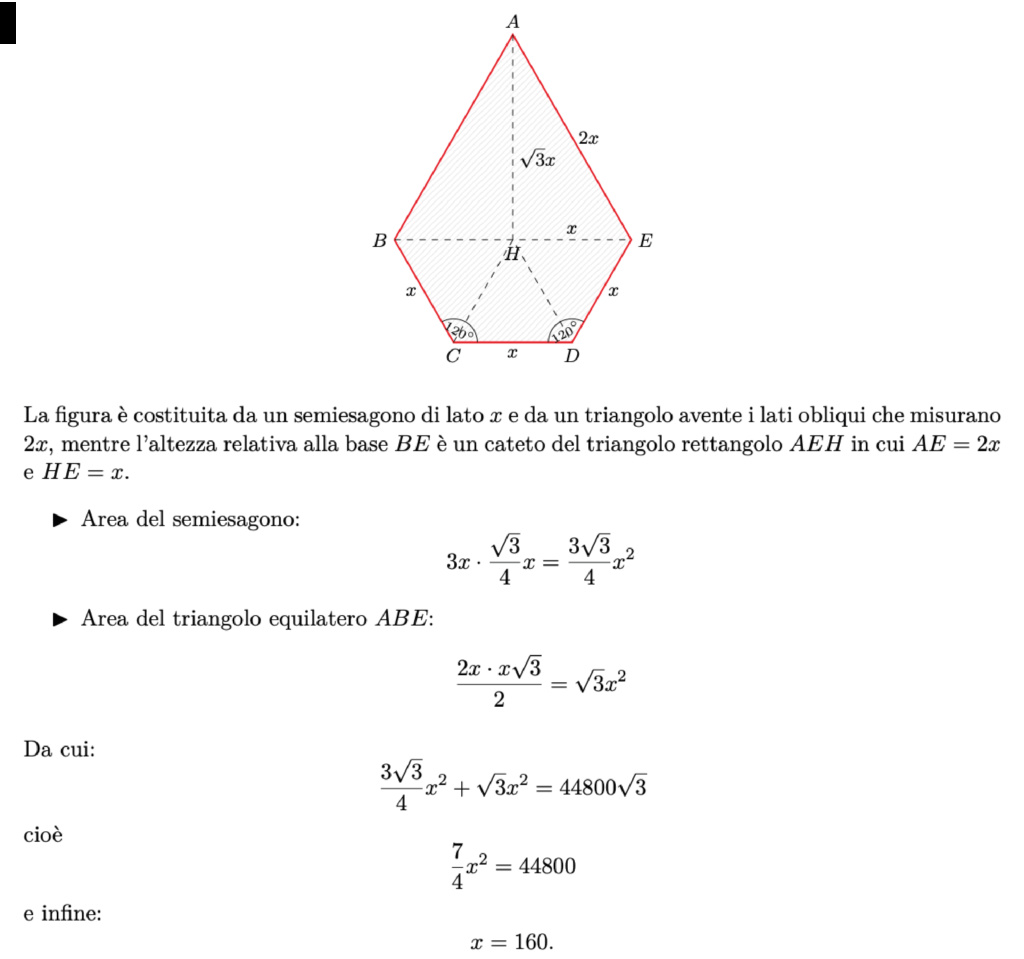
Tracciamo il segmento BE che divide il pentagono di area 44800√3 nel quadrilatero BCDE e nel triangolo BEA. Tracciamo inoltre i segmenti BD e CE che si intersecano in punto che chiamiamo O.

Consideriamo i triangoli isosceli BCD e CDE . Essi avendo due lati congruenti ( CD in comune , CD= DE =x ; CD=BC= x ) e l’angolo compreso di 120 ° ( B(C ) ̂D e C D ̂ E). Per il 1CC essi sono congruenti, in particolare CE= BD .

Consideriamo ora il triangolo DOC , esso è isoscele su base CD in quanto ha due angoli alla base congruenti di 30° ( E(C ) ̂D e BD ̂C) . Segue che OC=OD. Se CE=BD e OC= OD , BO= EO in quanto differenze di segmenti congruenti ( CE-OC = BD-OD).

Successivamente consideriamo Il triangolo isoscele BOE( BO= EO per quanto dimostrato precedentemente).
Esso ha BO ̂E = CO ̂D = 120° (in quanto opposti al vertice) e OB ̂E = OE ̂B = 30° .

Consideriamo infine gli angoli OB ̂E e BD ̂C congruenti di 30°, essi sono alterni interni rispetto alle rette BE e CD tagliate dalla trasversale BD , perciò BE // CD .
Possiamo quindi dire che il quadrilatero BCDE è un trapezio isoscele (BE // CD e (C ) ̂=D ̂=120° ) . La sua area sarà data dalla seguente formula:
((B+b)×H)/2 → ((BE+CD)×CG)/2

Tracciamo i segmenti di perpendicolare CG e DL e otteniamo i triangoli rettangoli BCG e DLE. Gli angoli CB ̂G e LE ̂D sono di 60° ( CB ̂D+ OB ̂E = CB ̂G = 60° e DE ̂C+ OE ̂B = LE ̂D= 60° ). Di conseguenza , i terzi angoli saranno di 30° (BC ̂G e LD ̂E).
Perciò BG =LE = X/2 ( BCG e DLE metà di triangoli equilateri, BC e DE ipotenuse e BG e LE lati opposti agli angoli di 30°).
Otteniamo così: BE= X/2 +X/2 +x = 2x ,
CG= √(x^2-(〖X/2 )〗^2 ) = X/2 √3
CD= x
L’ area del trapezio BCDE :

A= ( X/2 √3 × 3x ):2 = ( 〖3X〗^2/4 √3 )

Consideriamo ora il triangolo BEA: Esso è equilatero in quanto ha 3 lati di misura 2x ( BE, AB, AE ).
Tracciamo l’altezza AN che è sia mediana che bisettrice. La sua misura sarà :
AN= √(〖4x〗^2-x^2 ) = x√3

Calcoliamo dunque l’area di tale triangolo :
A= ((BE)×AN)/2 → ((2x)×x√3)/2 = x^2 √3

In conclusione ricaviamo x dalla seguente uguaglianza:

Area BCDE + Area BEA = Area ABCDE = 44800√3
↓
( 〖3X〗^2/4 √3 ) + x^2 √3= 44800√3
↓
Risolvendo questa equazione di secondo grado otteniamo che X= 160

Caro Mario,
ho seguito la tua dimostrazione. La parte sul trapezio onestamente mi è sembrata un po' ridondante. Per il resto bene.
Confrontati con quel che segue.