L'area di una strana mattonella

Nessuno si fa vivo? Vi è venuta qualche idea. Fatela conoscere.

Buonasera,
io (Federico Pampanelli) insieme a Mario Solinas e Giulio Franca abbiamo riprodotto il disegno su geogebra che allego.
Mario invierà a breve le considerazioni.

Buona sera signor Scorsipa: io, Federico Pampanelli e Giulio Franca abbiamo pensato di tracciare la retta passante per l'origine ( bisettrice del primo quadrante) e abbiamo notato che divide i seguenti quadrilateri ( i 4 verdi e quello rosso) In due parti simmetriche. Inoltre il quadrilatero rosso è un deltoide ( presenta due coppie Di lati consecutivi congruenti) perciò la sua area è ( diagonale maggiore × diagonale minore)/2. Ci mancano da trovare i vertici di tale deltoide per trovare l 'area. Ci faccia sapere se tali supposizioni sono corrette. Buona serata!

Ciao Federico e Giulio,
bene. Molto bene! 
Potete procedere. Sono sicuro che troverete il risultato.

Scusa Mariosol se non ti ho citato. Ciao dunque anche a te.

ci siamo riusciti: la somma dei fattori è 200 dato che la frazione è 81/119
entro oggi pomeriggio le invieremo a dimostrazione

Ottimo!! Siete dei grandi.

Bravissimi! Ce la faremo a trovare un esercizio che non sanno risolvere?

Salve Prof Scorsipa le inviamo la soluzione del problema sulla mattonella ( precedentemente avevamo inviato solo il risultato)


PROBLEMA: ” UNA STRANA MATTONELLA”

Soluzione proposta da Mario Solinas, Federico Pampanelli e Giulio Franca.

https://i.servimg.com/u/f67/20/20/95/54/la_str10.png

Risoluzione:
Tracciamo inizialmente la bisettrice del primo quadrante ( g1). Essa divide i seguenti quadrilateri ( i quattro verdi e quello rosso ) in due parti simmetriche .
In particolare il quadrilatero rosso è un deltoide in quanto ha due coppie di lati consecutivi congruenti ( OW≅ OB1 , B1P ≅ PW). La sua area sarà data dalla seguente formula:
A= (D1 × d2)/2 → (OP×B1W)/2
Consideriamo la bisettrice del primo quadrante ( g1) di equazione Y=X e la retta k di equazione Y=-6X +6. Mettendo a sistema le due equazioni abbiamo trovato le coordinate del punto d’intersezione O ( 6/7 ; 6/7 ), vertice del deltoide OB1PW.

Con un procedimento analogo abbiamo trovato le coordinate dei punti : P ( 3/2 ; 3/2 )
W (30/17 ; 12/17 )
B1 (12/17 ; 30/17 )



Successivamente abbiamo calcolato le lunghezze delle diagonali del deltoide :

PO = √(2×(3/2 )-6/7)2 = (9 ×√2)/14

B1W = √(2×( 12/17) - 30/17 )2 = (18√2)/17

Infine calcoliamo l’area del deltoide ( POWB1) :

A= ((9 ×√2)/14 × (18√2)/17 ) : 2 =81/119


Perciò la somma dei fattori della seguente frazione è uguale a 200 ( numeratore + denominatore )

OK. 
Gli altri compagni hanno seguito? 
Conoscete l'equazione segmentaria della retta?
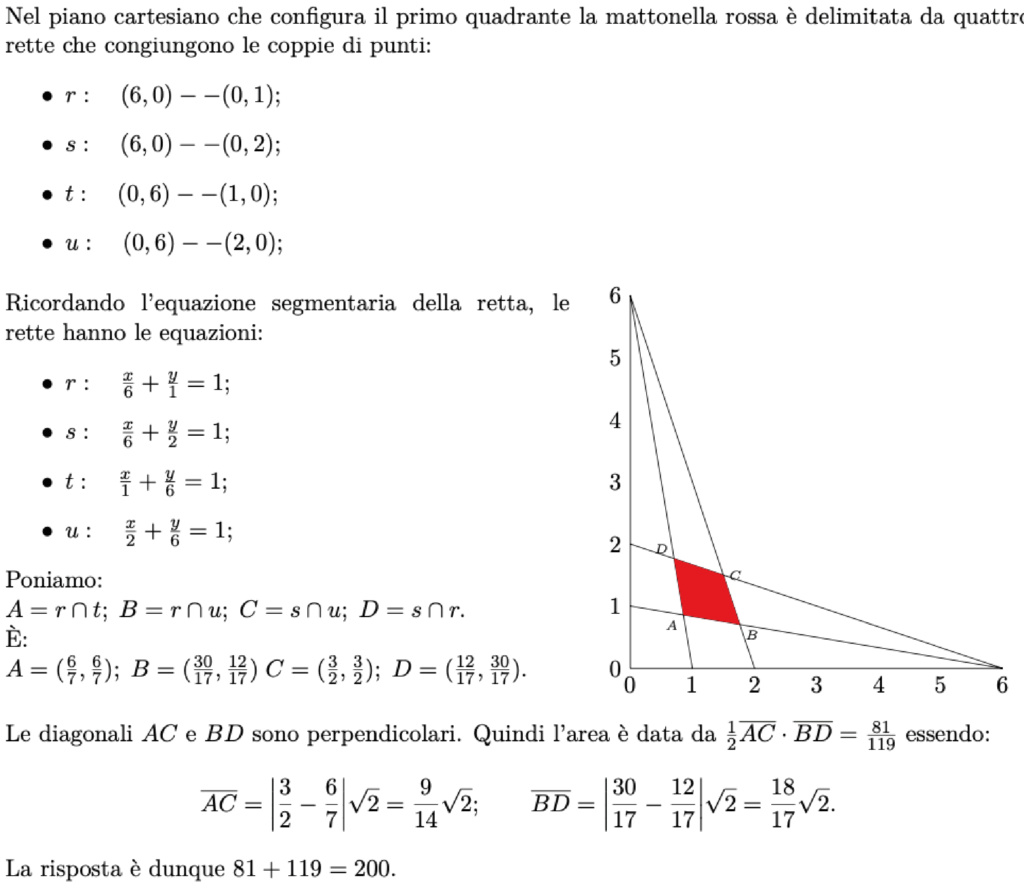
Se una retta taglia l'asse x in un punto si ascissa p e l'asse delle ordinate in un punto di ordinata q allora l'equazione della retta è data da:
x/p+y/q=1.
Nel caso nostro poteva essere molto comoda.
Ad ogni buon conto i miei complimenti!